addressing problem set mistakes

PS1 PS2 PS3

• matrix mechanics

PS4

• Morse potential vs. harmonic oscillator: the Morse potential does not have a minimum, so vib freq cannot be obtained for (certain molecules)
  • difference between Morse and HO?

MT

• to obtain ZPE corrected energy, its energy from MO calculation + ZPE
• BO approximation: separation of electronic motion and nuclear motion => molecular wavefunction that is product of nuclear wave function and electronic wave function
• LCAO-MO: MOs made of linear combination of AOs

PS5

• ratio of rates is e^{ΔE_a∘ − ΔE_b∘}RT

PS6

• how does the MO diagram show that the LUMO of the molecule is destabilized?
• bonding energy: final - initial (non bonded)
• why don’t MOs contain the coulomb and exchange integrals? is it just based on point groups?
• how did we get the point groups for CO

Review of Quantum Mechanics:

1. Schrodinger Eq. ✅
2. Relativity, Fermion and boson, Pauli exclusion principle ✅
3. Hermitian operator ✅
4. Dirac notation, basis set expansion, superposition of states ✅
5. Matrix mechanics ✅

Molecular Orbital Theory:

1. Born-Oppenheimer approximation, Nuclear and electronic Hamiltonians ✅
2. Atomic units, Potential energy surface (PES), Reaction coordinates, Transition states ✅
3. Basis sets ✅
4. H₂⁺ , Two-state model ✅
5. Electronic wavefunctions, Slater determinant ✅

Angular momentum:

1. Electron spin, Orbital angular momentum ✅

Group Theory:

1. Molecular symmetry, Point groups, Irreducible representations ✅
2. Construction of SALCs, Group theory, Character table ✅

Hartree-Fock Molecular Orbital Theory:

1. Variational theorem ✅
2. H₂, Hartree-Fock method ✅
3. Self-consistent-field Koopmans theorem ✅
4. Semi-empirical (H ̈uckel), Molecular mechanics ✅

Electron Correlation:

1. H2 dissociation problem, Configuration interaction, Coupled-cluster methods ✅
2. Perturbation theory ✅
3. Møller-Plesset perturbation theory ✅
4. Method comparison, Accuracies, Convergence issues ✅

Density Functional Theory:

1. Hohenberg-Kohn theorems, Kohn-Sham method ✅

Lectures

2 Python and QM Intro

• slater vs. gaussian
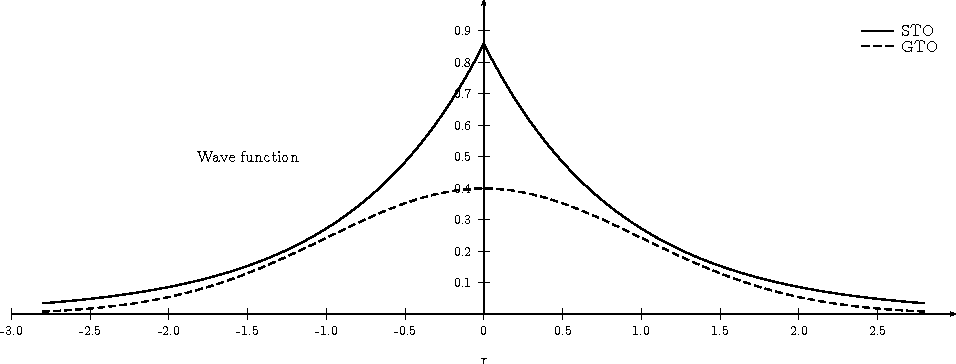
  • gaussian decays too quickly and has longer tails
    • ill behaving because decays too fast
    • near nuclei (at origin), is flat, differential is 0
  • slater is proper function to use
    • not differentiable because of cusp (at origin)
  • predict different behaviour at nuclei (experimentally by EPR)
    • should anticipate some mistakes
• review 6 ways non-differentiability

notes on relativistic effects

• special relativity: laws of motion for non-accelerating bodies travelling at speed of light
  • as speed approach 0, special relativity tends towrds eq with newton’s laws of motion
• general relativity: laws of motion viewed from accelerating reference frames (geometric explanation for gravity)
• special relativity:
  • postulates
    1. impossible to transmit information faster than speed of light
    2. laws of physics are identical, without any variation, in every location in universe, no matter how fast travelling
  • consequences: time dilation (observer in one reference frame observes clock in another frame to be ticking more slowly than in observer’s own frame), length contradiction (same analogy but with length), and as a body moves with increasing velocity its mass increases: t = γt₀, 𝓁 = γ𝓁₀, m = γm₀
    • this follows E = mc², E² = p²c² + (m₀c²)²
• combining relativity and quantum theory
  • energy “uncertainty” (QM) mass-energy equivalence (special relativity) → particle/anti-particle pairs by quantum fluctuations
  • klein-gordon equation (relativistic version of Schrodinger equation for spin-0 particle) (using time-dependent Schrodinger equation) $$\begin{align*} E &= \frac{p^2}{2m} \\ i\hbar \frac{\partial}{\partial t}\psi &= - \frac{h^2}{2m} \nabla \psi \\ (i\hbar \frac{\partial}{\partial t})^2 \psi &= - [(i\hbar \nabla)^2c^2 +m_0^2c^4] \psi \\ \frac{1}{c^2}\frac{\partial^2}{\partial t^2} \psi - \nabla^2 \psi + \frac{m^2_0c^2}{\hbar^2} \psi &= 0 \\ \end{align*}$$ this is the d’Alembert operator (???)
• dirac equation:
  • electron is spin 1/2 particle (fermion) $$ih\frac{\partial \psi(X, t)}{\partial t} = (c\sum_{k=1}^{3} \alpha_k p_k + \beta mc^2) \psi(x,t)$$ factorized using d’Alembert operator $$\psi(x,t) = \begin{pmatrix} \psi_1(x,t) \\ \psi_2(x,t) \\ \psi_3(x,t) \\ \psi_4(x,t) \\ \end{pmatrix} $$
  • wavefunctions 1/2 are for particle and 3/4 are for antiparticle (each wavefunction is either spin-up or spin-down)
    • we get gamma (dirac) matrices and pauli matrices
• Taylor expansion → power series a₀ + a₁x + a₂x² + etc
  • different powers of x form basis set
  • chem312: ψ(x) = ∑C_nψ_n
  • minimal basis set is least accurate
• spin multiplicity: 2s+1 (review term symbols)
  • 1 e, s = 1/2
  • 0 single electrons, s = 0, 2s+1 = 1
  • open shell singlet: 1/2, -1/2
  • open shell triplet: 1/2, 1/2
  • closed shell triplet is not possible (Pauli exclusion principle)
• hybridization changes electronegativity
  • https://web.ics.purdue.edu/~loudonm/pdf/Supplement_04.01.pdf
  • sp more electronegative than sp² more electronegative than sp³
  • this causes dipole moments: arrow goes + to -
  • sp² has electron in the 2p orbital, which the electron density of 2p is not evenly distributed around nucleus in all directions
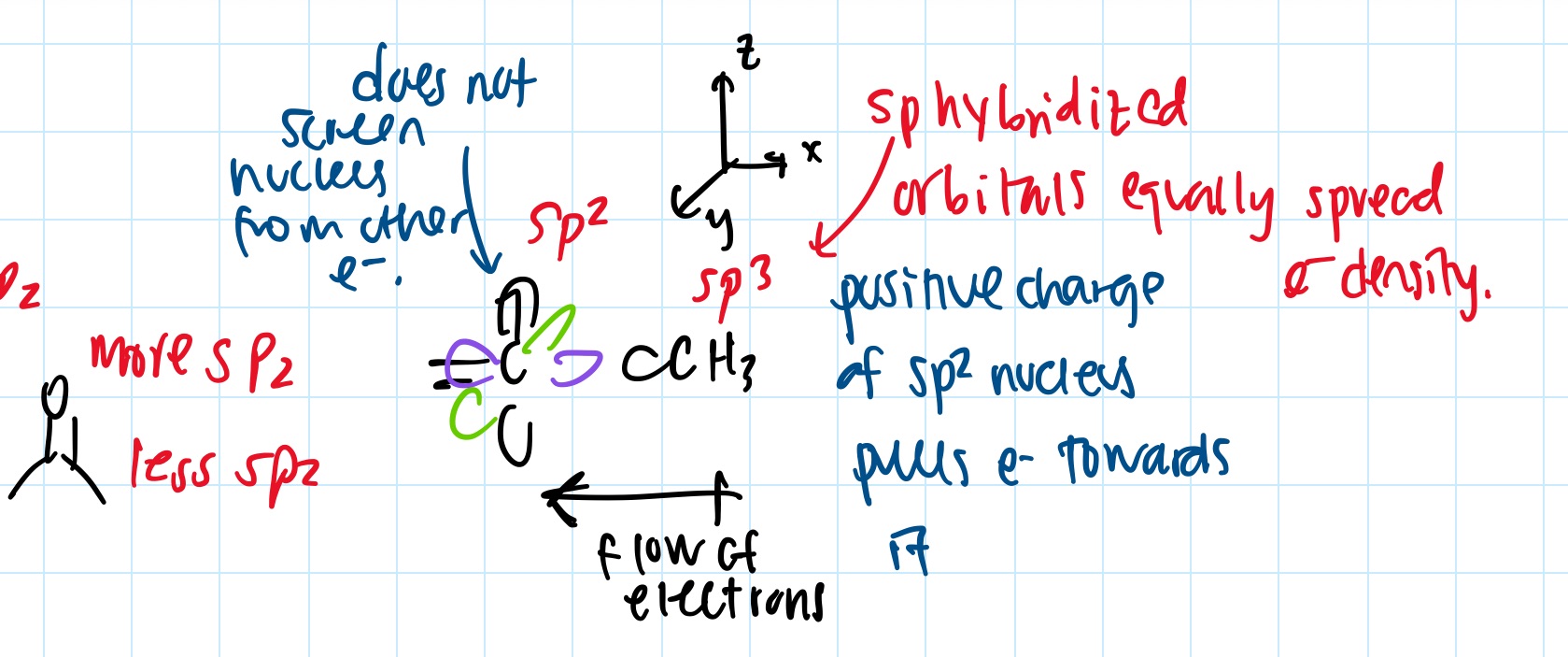
  • sp³ by contrast, the electron density is evenly distributed in the hybrid orbitals
• geometry sequence energies: tries to find a derivative of 0 to minimize nuclear repulsion energy
  • derivative is indication of force
• basis functions: relate to the orbitals, stay the same for each bond distance the program tries
• molecular energy vs. geometry optimization: ME is more optimized because geometry optimization doesn’t take derivative to 0, only closely

ĤΨ = EΨ, where the Hamiltonian Ĥ = T̂ + V̂

• by substituting classical momentum with its quantum form: $$\hat{T} = -\frac{\hbar ^2}{2m}\nabla^2$$
• potential operator V̂ if function of position r and time t.
  • don’t care about gravity because it is too small
  • Coulombic interaction: $$\hat{V} = - \frac{1}{4\pi\epsilon} \frac{e^2}{r}$$
• |Ψ|²: charge density, gives information about dipole moment and chemical reactivity
• PES: energy, E, an eigenvalue. potential energy surface
  • give you information about stable molecular structures/chemical reactivity

3 Relativity, Boson, Fermion

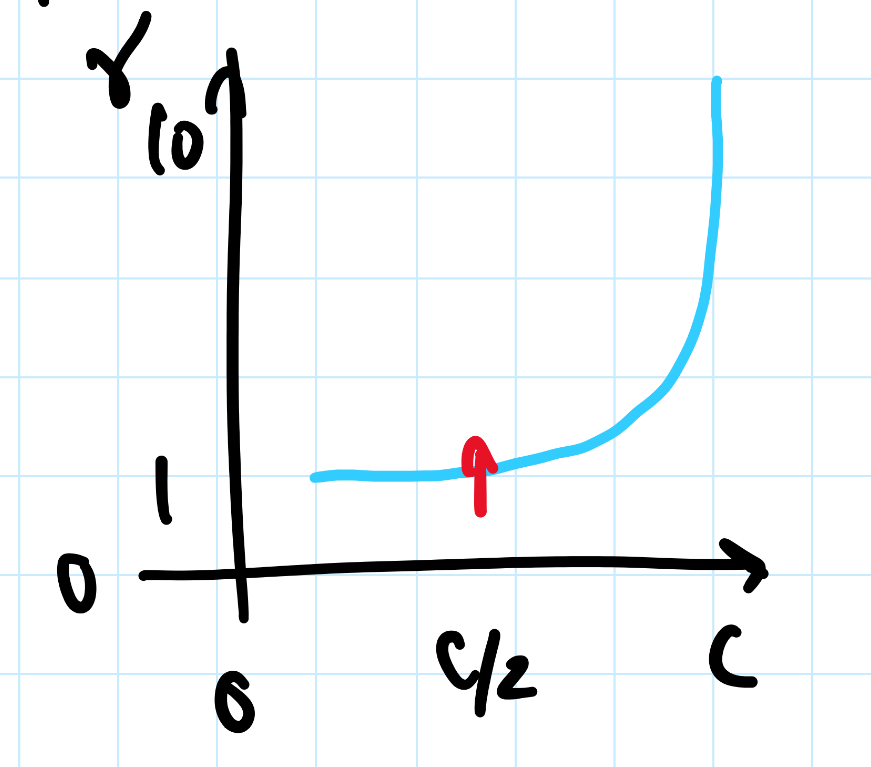
relativity causes

• intrinsic spin
• pauli exclusion principle, linked with electronic spin
• spin-orbit coupling
• orbital motions create magnetic fields -> solved by perturbation theory

noone can travel faster than the speed of light: |v| ≤ c

• $$0 \leq \frac{|v|}{c} \leq 1$$
• lorentz factor: $$\gamma = \frac{1}{\sqrt{1 - (\frac{v}{c})^2}}$$

length contraction:

• only happens in dimension of velocity
• the faster the object moves, the shorter the object becomes
• subjective: depends on how fast the observer is moving

mass increase:

• mass in motion appears more massive
• at speed of light can’t move anymore (so massive)
• the faster it moves, the more massive it becomes

time dilation:

• things that have short half life: live forever when moving at speed of light

core electrons: more stable

• s,p orbitals contract in size
  • screen the nuclear charge
  • smaller in size means lower energy, denser electron cloud
  • move faster??
    • heavier so more kinetic energy?
• p, d orbitals larger because feel less nuclear charge
• http://alchemy.cchem.berkeley.edu/inorganic/RelativisticEffects.pdf

fermion: half integer spin

• electron, neutron, proton, quark
• even number of fermion is boson, odd number of fermion is fermion
• spin in half units of ℏ

boson: integer spin

• spin in integral units of ℏ

Pauli Exclusion Principle

• electrons in an atom: no two electrons can have the same quantum numbers
• molecules: only two electrons can occupy a molecular orbital, with opposite spins
• for two identical fermions, total wavefunction is antisymmetric

4 Postulates in QM

1. well behaved wavefunction describes the state of the system
   • phase factor Ψeⁱ⁰

• function must constrain to physical world

1. any observable A, has Hermitian operator Â

• Hermitian operators are self-adjoint

1. time dependent Schrodinger equation
   • we use time independent equation (time is e^−iEt/ℏ)

5 Dirac notation, basis set expansion, superposition of states

dirac notation

• adjoint: ⟨f|Â = ⟨Â^†f|
  • conjugate transpose
• Hermitian: Â = Â^†
• side note: transpose of $$\frac{\partial}{\partial x}$$ is not naively simple!
• expansion of state
  • complete set, k goes to infinity

closure

• how to use closure for orthonormal complete set

Ĉ = Σ_k = 1^inf|k⟩⟨k| = 1

• use like an operator
• eigenfunctions of any Hermitian operator form orthonormal complete set
  • {ψ_k(k = 1, 2, 3, ..,)} with ⟨ψ_i|ψ_j⟩ = δ_ij
  • since closure is equal to 1, any state |Ψ⟩ can be expanded as linear combination using complete set

LCAO: how does it differ from

• basis set is non-orthogonal, finite, on different nuclei
• accuracy depends on basis set used

6 Matrix mechanics

• determinant: det(A^T) = det(A)
• m rows, n columns
• matrix mechanics:
  • with a complete basis set (how would you represent with matrices)
    • bra: row vector
    • ket: column vector
    • ⟨Ψ|^† = (c₁^*, c₂^*, c₃^*, ...)^†=|Ψ⟩
    • |Ψ⟩^† = ⟨Ψ|
  • orthonormal basis set (δ_ij):
  • non orthogonal basis set (⟨ψ_i|ψ_j⟩ = S_ij ≠ δ_ij)
    • overlap matrix = S
    • S = S^†
• operator with basis set ⟨ψ_i|Âψ_j|⟩
• adjoint Â^† with basis set
• euclidean 3D vector space vs. Hilbert nD metric space

7

8

9

• notes from paper and ipad notes summary

bonding between 2 different atomic orbitals on 2 different atoms

$$\Psi_{bonding} = \begin{pmatrix} 1 \\ \alpha_1 \end{pmatrix}$$ $$\Psi_{antibonding} = \begin{pmatrix} -\alpha_2 \\ 1 \end{pmatrix}$$

• α₁ ≠ α₂: this means the interaction creates to MOs of two different energy differences α₂ > α₁ > 0
  • there is more destabilization vs. stabilization
  • the lower energy atomic orbital is the one that is more electronegative, why? because holds electrons more close to the nucleus, less separation between negative and positive charges
• with ϵ_n = AO energy, when far apart, E₁ → ϵ₁ and Ψ → ψ
• as the difference between two atomic orbital energies increase, bonding interactions decrease, why? mathematically: $$E_1 = \epsilon_1 - \frac{\epsilon_2 - \epsilon_1}{2(1 - S^2_{12})}(\sqrt{1 + 4\alpha_1\alpha_2} - 1 - 2\alpha_1S_{12})$$, so when the difference between ϵ₂ − ϵ₁ is very large, then there is no bonding.
• the chemical result we can get from this is that: AOs close to each other feel bonding interaction and are affected, AOs with different energy levels remain non-interacting
• this is why we only get certain types of mixing/hybridization: the AO energies must be close enough
• atomic orbitals contribute unevenly to MOs: antibonding is destabilized slightly more than stabilized

molecular hamiltonian

• hamiltonian is total energy operator
• for a molecule:
  • N nuclei: (α = 1, 2, 3, ..., N) with (mass M_α, charge Z_αe, position R_α)
  • n electrons: (i = 1, 2, ..) with (mass m_e, charge −e, position r_i)
• Hamiltonian Ĥ = T̂_N + T̂_e + V̂_NN + V̂_ee + V̂_Ne
  • after applying the (hartree) atomic units, simplified down to:
    • nuclear kinetic: $$\hat{T}_N = -\frac{1}{2} \Sigma_\alpha \frac{1}{M_\alpha} \nabla^2_\alpha$$
    • electronic kinetic: $$\hat{T}_e = -\frac{1}{2} \Sigma_i \nabla^2_i$$
    • nuclear repulsion: $$\hat{V}_{NN} = \Sigma_{\alpha < \beta} \frac{Z_\alpha Z_\beta}{R_{\alpha\beta}}$$
    • electronic repulsion: $$\hat{V}_{ee} = \Sigma_{i < j} \frac{1}{r_{ij}}$$
    • electron-nuclear attraction: $$\hat{V}_{Ne} = \Sigma_{\alpha, i} \frac{-Z_\alpha}{r_{\alpha i}}$$

born-oopenheimer approximation

• the nucleus is much much more massive than the electron
• can separate motions of electrons and nucleus
  • electrons move with frozen geometry with nuclei fixed in space (what does it mean to move with fixed geometry)
    • when nuclei move, take calculations again
• total molecule: $$\hat{H}_{total} = \hat{T}_N + \hat{\textbf{T}}_e + \hat{V}_{NN} + \hat{\textbf{V}}_{ee} + \hat{\textbf{V}}_{Ne}$$
• we get the electronic hamiltonian with fixed nuclear parameters (framework): Ĥ_e = T̂_e + V̂_ee + V̂_Ne
  • Ĥ_eψ_k = E_kψ_k, ψ_k({r_i}; {R_α})
  • then we get Ψ_total from expanding the basis set of electronic wavefunctions |Ψ_total({r_i}, {R_α})⟩ = Σ_kϕ_k({R_α})|̇ψ_k({r_i}; {R_α})
    • ϕ is nuclear, Ψ is electronic
    (T̂_N + V̂_NN + Ĥ_e)Ψ_total = E_totalΨ_total⟩

adiabatic and BOA

• resulting BOA is still hard to solve: basis function (i think) $$(\hat{T}_N + E_l + \hat{V}_{NN})\phi_l + \Sigma_k \{ \phi_k \langle |\hat{T}_N |\rangle + \Sigma_{\alpha = 1} \frac{\langle|\hat{P}_\alpha |\rangle \hat{P}_\alpha \phi_k}{M_\alpha}\} $$
• adiabatic: hopping between different electronic states is eliminated: only ϕ_l stays
  • to change quantum state, requires heat (T̂_N + E_l + V̂_NN)_ϕl + ϕ_l⟨ψ_l|T̂_N|ψ_l⟩ = E_totalϕ_l
    • if nuclear framework doesn’t move around, then second term is 0
• that is the BOA: nuclear framework does not move: (T̂_N + E_l + V̂_NN)ϕ_l = E_totalϕ_l
  • this is RHF energy: restricted hartree fock energy
  • electrons move and nucleus does not
• potential energy surface folows from BOA: T̂_NN + V({R_α})ϕ({R_α}) = E_totalϕ({R_α})
  • there is no kinetic contributioN?
  • we need V({R_α}) = E_l + V̂_NN or the curve looks weird, there will be no minimum
    • contains all electgronic motions
    • nueclei move on PES, because we are shortening the distance between nuclei
      • PES gives net forces felt by nuclei due to complex motions/coulomb interactions of electrons
• electrons move so fast, not point to talk about electron motion
  • but shrodinger equation coupoles motion between electrons and nueclei
• BOA provides theoretical basis for existance of chemical structures
• BOA drawbacks:
  • independent of nuclear masses, PES for isotopes is the same
    • this implies electronic statse should be independent of particular isotopes of nuclei
      • but different isotopes change electronic structure as non-adibatic coupling terms depend on nuclear mass

10

lecture notes:

• polyatomic DOF: 3N
• the potential energy surface incorporates all types of energy (translational, rotational, vibrational)
• upper PES: repulsive, minimum is attractive representing a bond
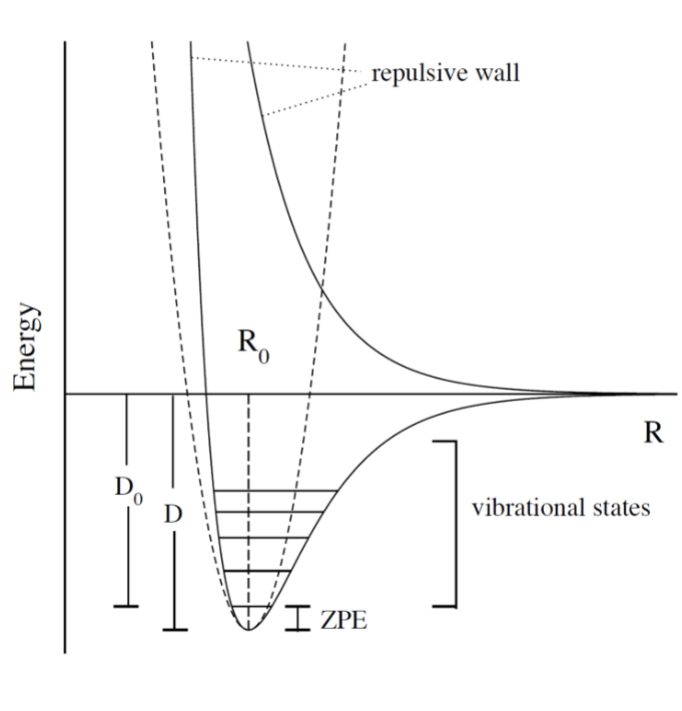
• ZPE (zero point energy): for translational and rotational is 0 energy at 0K. But vibrational:
  • $$ZPE = \frac{1}{2} \hbar w$$
  • true ground state energy is D₀ = D − ZPE
    • why minus ZPE? and why is D₀ the true GSE?

potential energy surfaces (PES)

• a molecule needs 3N coordinates to describe it
  • position (spatial): 3
  • rotations: 3 (2 for linear)
  • (internal degrees of freedom) vibrational: 3N - (3 + 2 or 3)
    • PES is described using these coordinates

• classifications
  • ab initio: from first principles
    • only need electronics Ĥ_e: number of electrons and type of nuclei
  • empirical: functions constructed from values by fitting calculated properties to experimental data
    • Lennard-Jones PES: $$V_{LJ}(R) = V_0 [(\frac{R_0}{R})^12-2(\frac{R_0}{R})^6]$$
      • V₀ and R₀ are well depth and minimum of potential well respectively; determined from IR
        • functional form: chemical intuition
        • parameters: experimental
    • semi-empirical: mixture
• 412: concerned with ab initio
• larger molecules use empirical potentials
• anatomy of PES
  • attractive state: has a well representing a bond
  • repulsive state: no stable bond, not really a well, like a ball rolling down until reaching dissociation limit
  • R → 0: PESs climb to higher energies because of electron cloud repulsion and then more steeply from nuclear repulsive term
• Gaussian finds R₀, at the minimum of PES
  • matches experimental structure at low vibrational states
• vibrational analysis
  • approximations based on harmonic oscillator
    • approximated in Taylor series, which we can simplify to parabola
      • matches behaviour at the well, but elsewhere does not
    • approximation has 5-10% difference from experimental values; even with exact PES using the harmonic approximation will lead to errors
• how is this done for a PES of p dimensions:
  1. find stationary point where all first derivatives are 0 (makes taylor series expansion simpler?)
  2. expand PES in multidimensional Taylor series about stationary point keeping only quadratic term (linear terms 0 because of step 1.)
  3. form Hessian matrix, where diagonals are pure second derivative and everything else is mixed second derivative.
  4. diagonalize the Hessian to find new set of coordinates, which are normal modes, q_i.
     • q_i is a linear combination of original {R_i} coordinates.

1. in normal mode basis, only pure second derivatives remain. mixed second derivative terms are zero; no coupling between different normal modes. each normal mode is independent of others, so the pure second derivative can be used to define a harmonic oscillator
   • p normal modes, p harmonic oscillators
2. ZPE is sum of harmonic frequencies multiplied by $$\frac{\hbar}{2}$$

side notes:

• normal modes are uncoupled, unlike bond coordinates; exciting one normal mode doesn’t affect other normal modes
• can use symmetry to simplify calculations regarding normal modes
• must use same method and same basis set to perform vibrational analysis as was used for geo opt; different methods approximate different stationary points
• normal modes used to characterize stationary points (?).

crossing and non-crossing PES

• NaCl: at limit of R goes to infinity; covalent bond does not have minimum, while ionic bond has minimum
  • these two graphs cross: PESs obtained with Born-Oppenheimer approximation
    • total wavefunction is product of nuclear and electron
  • in real system, there are interactions with the two PESs and there is no crossing: avoided crossing point: non-Born-Oppenheimer effect
    • total wavefunction is linear combination of ψ_electron^ion and ψ_electron^covalent, with some expansion coefficients

reaction paths, transition states and intermediates

• 1D path, single normal mode
• PES for 2D case: TS is saddle point
• perpendicular modes: not along reaction path, bound vibrations
  • normal mode frequencies are positive numbers
• important to include ZPE into calculations of energy because of exponential dependence upon ΔE^t
  • ZPE only uses positive normal mode frequencies

diabatic and adiabatic processes

• adiabatic theorem: QM system subject to gradually changing systems can adapt it’s functional form
• diabatic: rapidly changing conditions prevent system from adapting its configuration, so probability density remains unchanged? no eigenstate of final Hamiltonian with same functional form; system ends in linear combination of stats that sum to reproduce initial probability density
• adiabatic: gradually changing allow system to adapt configuration, probability density is modified. starts in eigenstate of initial Hamiltonian and ends in eigenstate of final Hamiltonian.

11

• ZPE (zero point energy): for translational and rotational is 0 energy at 0K. But vibrational:
  • $$ZPE = \frac{1}{2} \hbar w$$
  • true ground state energy is D₀ = D − ZPE
    • why minus ZPE? and why is D₀ the true GSE?
      • ZPE is always bigger than 0
    • D₀ represents energy to break a bond, enthaply required to break a bond:
      • AB → A + B
      • ΔH = (H(A) + H(B) − H(A − B)) = (E_diss + E_dissZPE) − (E_bond + E_bondZPE) = −(E_bond − E_bondZPE)
• frequencies: positive represents stationary state (minimum), negative represent transition state (maximum)
  • for a true transition state, you can either go back or to the final product, so there will be only one negative (or imaginary) frequency
    • negative frequencies not included in ZPE
• Morse vs. Harmonic: at higher quantum states, the differences are too large, harmonic is less accurate

PES interactions

• BOA: predicts crossing (why?) because the equatio is single product?
  • single product may break down and not correctly describe total wavefunction
  • what does it mean to be fixed by ZPE?
  • contradicts the existance of sodium ions and elemental sodium
• non BOA: avoided crossing Ψ_total = c_ionΨ_total^ionc_covΨ_total^cov

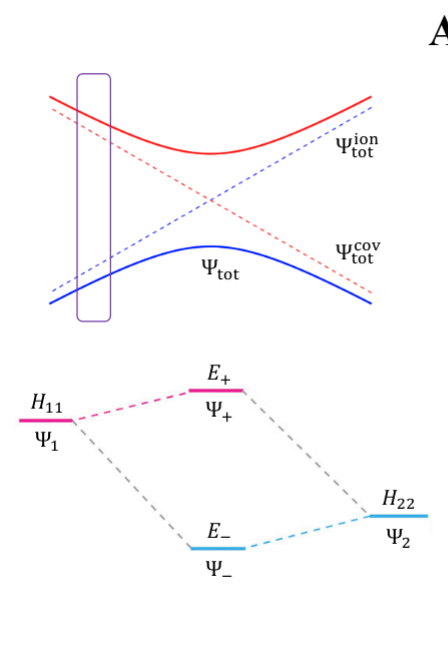
• from the hamiltonian matrix, if $$$H_{12} = 0$, then PES crossing happens with no problem - this happens when $$Ψ₁andΨ₂$$ are different spins or point groups

adiabatic and nondiabetic processes

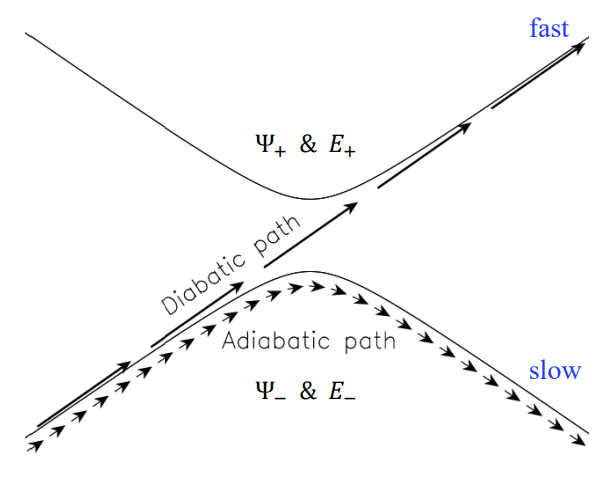
• fast: mixed states on upper and lower PESs
  • Ψ_d = c₊Ψ₊ + c₋Ψ₋
  • E_d = |c₊|²E₊ + |c₋|²E₋
• slow: process ends up in pure state in lower PES
  • Ψ_a = Ψ₋
  • E_a = E₋

quiz questions

• breaking bonds fast or slow means changing the motion of the nuclei fast or slow
• fast bond breaking by shooting strong, intense laser
• vibrational frequencies: at TS only one vib freq is imaginary (or negative)
• PES crossing: depends on the interaction energy, represented by H₁₂

12

• STO orbitals: mimic nodeless radial components of H-like orbitals
  • χ_lm^STO = Nr^le^−lrY_lm(θ, ψ)
• GTO orbitals: approximate nodeless radial components of H-like orbitals
  • χ_lm^GTO = Nr^le^−lr2Y_lm(θ, ψ)
  • can convert Y_lm in GTO to cartesian coordinate, no more complex numbers (i think)
  • for matrix calculations, GTO is more stable, and easier to calculate
• how to approximate different types of bonding:
  • non polar covalent: can use neutral H-like orbitals
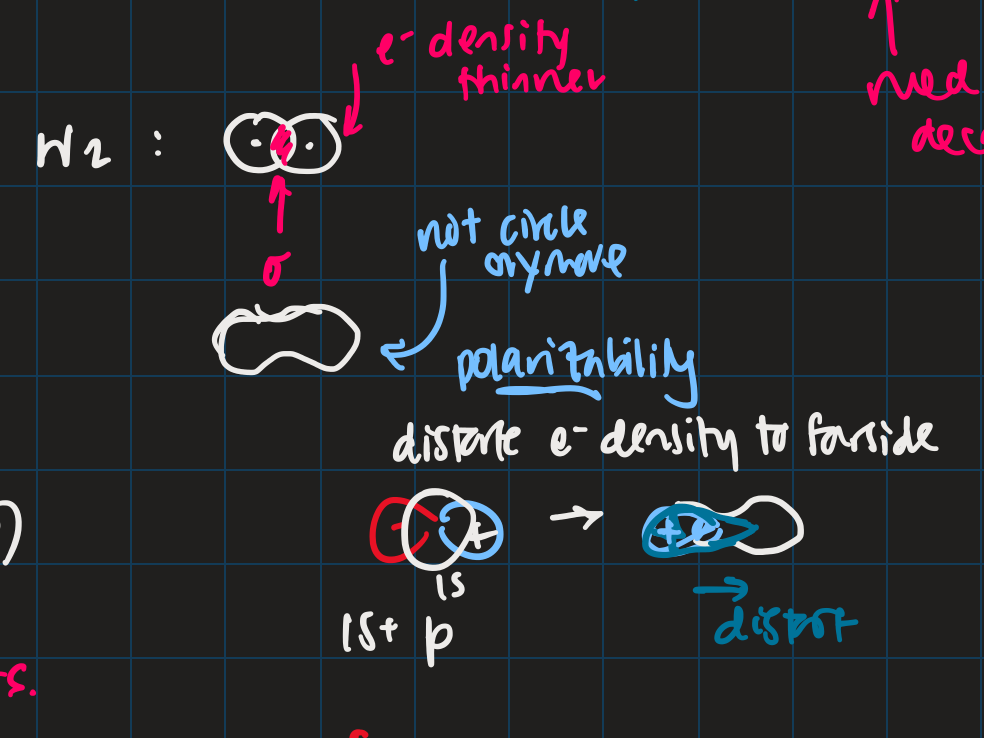
  • polar covalent: cation-like behaviour, electron cloud is thinner, neutral H-like orbitals decay too slowly
  • ionic: cation-like behaviour, electron cloud is thinner, neutral H-like orbitals decay too slowly
  • hydrogen bonding: extended range intermolecular forces, neutral H-like orbitals decay too quickly
• polarization
  • H₂ bonding is not just two s-orbitals overlapping, more like a peanut shape
  • usually use orbital with +1 angular momentum

• CGTOs: linear expansion of PGTOs
  • χ_k^CGTO = Σ_a = 1^n_cc_a^kχ_a^PGTO
• types of basis sets:
  • minimal: one GTO/CGTO per AO
  • double-zeta: 2 basis function per AO
  • triple-zeta: 3 basis function per AO
  • split-valence: minimal basis for core atomic orbitals, larger basis for valence atomic orbitals
• common GTO basis sets
  • representation: {core minimal} - {valence} {++} G {nd,p}
    • {core minimal}: if this is a number, represents the number of PGTOs used to represent the core electrons (is this n PGTOs for all AOs that are core?)
    • {valence}: the zeta of PGTOs that make up the CGTOs for valence electron AOs
    • {++}: one plus means diffuse function for heavy atom, two plus mean diffuse function for heavy atom and hydrogen
    • {nd, p}: polarization functions, nd for heavy atoms, p for hydrogen
• basis set size vs. computation time: O(n⁴)$
• BSSE: for relative energies, same method/basis set must be used for all calculations, or BSSE can arise with accessible basis sets differ in 2 calculations.
• diffuse: long-range, polarization: bonding

different basis set

GTO	Quality	Row-1	Row-2	Row 3	Interpretation
STO-3G	minimal	(3s) → [1s]	(6s,3p) → [2s,1p]	(9s, 6p) → [3s, 2p]	3 PGTOs for 1 CGTO, 1 CGTO per 1 AO
3-21G	basic	(3s) → [2s]	(6s, 3p) → [3s,2p]	(9s, 6p) → [4s, 3p]
6-311+G(2d,p)	accurate	(5s, 1p) → [3s, 1p]	(12s, 6p, 2d) → [5s, 4p, 2d]	(14s, 11p, 2d) → [7s, 6p, 2d]

basis sets

• spatial part of spin orbital expressed as linear combination of atomic orbitals
• natural expand MOs in terms of AOs
  • hydrogen-like atomic orbitals (time consuming)
  • ab initio MO theory: Slater-type orbitals (STOs) or Gaussian-type (GTOs) are used as basis sets

hydrogen-like atomic orbitals

• solution of following equation: $$(-\frac{1}{2}\nabla^2 - \frac{Z}{r}) \psi(r) = E \psi (r)$$
  • in spherical coordinates: ψ_nlm(r, θ, ρ) = R_nl(r)Y_lm(θ, ρ)
• slater-type orbitals: expressed in spherical coordinate system
  • χ_nlm^STO = NY_lm(θ, ρ)r^n − 1e^−ζr
  • exponential decay at long range, Kato’s cusp condition at short range, no radial nodes
    • not convenient numerically: integral evaluation over STOs done numerically (why does this introduce error)
    • Kato’s cusp condition: electron density has cusp at position of nuclei
• gaussian-type orbital (also in spherical coordinate system):
  • χ_nlm^STO = NY_lm(θ, ρ)r^{2n − 2 − l}e^−ζr2
  • can be evaluated with analytical formulae (Gaussian Product Theorem): product of two GTOs centered on different atoms is finite sum of Gaussian functions centered on point along axis connecting them: saves time and elimiates error in determining matrix elements
    • incorrect physical behaviour of GTOs: decays much faster for large r.
    • do not satisfy Kato’s kusp condition
  • instead use contracted sets (CGTOs) of primitive GTOs (PGTOs) normally used: $$\chi^{CGTO} = \sum^k_i a_i \chi^{PGTO}_i$$
    • for STO-3G: three PGTOs form each CGTO to mimic one STO

comments:

• core orbitals contribute most of overall energy but least to chemical bonding, valance orbitals most important chemically but contribute little to overall energy
  • basis functions constructed in a way to describe valence orbitals energies better than core orbitals
  • absolute energies quite off, but relative energies are accurate
    • need to use same method and basis set for all calculations
• basis set superposition error: accessible basis sets different in two calculations
  • when two calculations have different basis function space, the calculation with larger basis function space will
    • add ghost molecules to account for BSSE (CP method)
    • present in almost all calculations

more on basis sets (additional)

• expanding MO in set of known functions is not an approximation if basis set is complete (infinite)
  • unknown MO is function in infinite coordinate system spanned by complete basis set
• finite basis: only components along coordinate axes corresponding to basis set is represented
• smaller the basis, the worse the accuracy, the better a single basis function is, the fewer basis functions are needed
  • computational scaling: M⁴

1. slater and gaussian type orbitals (type of AO)

   • STOs (polar coordinates):
     • no radial nodes
       • introduced through linear combinations
     • exponential dependence:
       • mirrors exact orbitals for hydrogen
       • fairly rapid convergence
     • used for atomic/diatomic systems where high accuracy desired
   • GTOs (polar or cartesian):
     • sum of l_x, l_y, l_z determines type of orbital
     • there are different number of components for spherical functions (6 for d) and 5 for d in cartesian coordinates
       • can transform cartesian components to spherical functions
   • use of only spherical components reduces problems of linear dependence for large basis set
   • r² makes GTO inferior to STO in two ways:
     1. at nucleus, GTO have zero slope, when STO has cusp, so GTOs have problems representing behaviour near nucleus
     2. GTO falls off too rapidly far from nucleus compared with STO, and tail of wave function is represented poorly
   • because GTO is less accurate, when making basis sets, more GTOs must be used to achieve same level of accuracy that can be achieved with less STOs (3 GTOs per STO)
     • but computational of integral of GTOs is easier
   • GTOs preferred for computationally efficiency
     • most applications take GTOs to be centred at nuclei
       • for some calculations: centre of basis function may not be center of nucleus

2. classification of basis sets

   • how many functions to be used?
   • minimum basis set: only enough functions to contain all electrons of neutral atom
     • H to He: single s-function
     • Li to Ne: 1s function, 2s function, 3 2p functions
     • Na to Ar: 1s function, 2s function, 3 2p functions, 3s function, 3 3p function
   • double zeta: doubling of all basis functions
     • demonstrate importance with HCN:
       • C-H bond: hydrogen s orbital (H) and p_z orbital (C)
       • C-N pi bond: p_x and p_y orbitals of C and N
         • pi bind will have more diffuse electron distribuion than C-H sigma bond
           • minimum basis set: comprimize will be made
           • DZ: tighter function can enter C-H bond with large coefficient, diffuse function (small exponent) can be used for C-N pi bond
     • split valence basis: only doubles valence orbitals (VDZ)
   • triple zeta: tripling of all basis functions, also triple split valence basis set
   • higher angular momentum functions -> polarization functions, also important
     • electron distribution along bond is different than perpendicular to bond
     • for H-C bond, if only s functions are described, then electron density perpendicular cannot be described
       • add set of p-orbital functions to H, then p_z component can be used to describe perpendicular electron density
         • p-orbital introduces polarization of s-orbitals
   • for single determinant wave function: first set of polarization functions is most important
   • electron correlation: energy lowering by electrons “avoiding” each other
     • “in-out”: radial correlation, one electron is close to and the other, far from nucleus
       • wavefunctions with different exponents
     • “angular correlation”: two electrons on opposite side of nucleus
       • same magnitude exponents but different angular momenta
   • adding single set of polarization functions (p-functions on hydrogen, d-functions on heavy atoms): double zeta plys polarization
   • basis set balance: having too many polarization functions vs. small basis set is not good
     • mixing of basis sets: minimum basis on spectator ions and DZ on interesting parts
     • or polarization functions on important hydrogens -> creates artefacts
     • use of small basis sets for systems containing very different numbers of valence electrons may produce artefacts

3. even and well tempered basis sets

13

14 MO Theory

15 slater determinant for N-Electron wavefunction

• made from orthonormal spin orbitals: {ψ_a^SMO} with ⟨ψ_a|ψ_b⟩
• we get N × N matrix, where N is number of electrons,

$$\Psi(1,2,..,N) = \frac{1}{\sqrt{N!}} \begin{vmatrix} \psi_a(1) & .. & \psi_a(N) \\ \psi_c(1) & .. & \psi_c(N) \end{vmatrix}$$

• where rows are orbitals and columns are electrons.
  • applying permutation operator (change position of electrons) makes the resulting wavefunction antisymmetric
• properties of determinants:
  • interchanging two rows or two columns: rows(move electron to another spin orbital, flipping spin?), columns (moving electron positions) reverses the sign
  • equating two rows or columns: putting two electrons as same spin (row) or putting another electron into same orbital as another electron, 0 because not valid
• shorthand
  • Ψ(1, 2, N) = |ψ_a(1), ψ_b(2), ...ψ_c(N)⟩
  • pauli principle: pauli antisymmetric principle and pauli exclusion principle
  • properties:
    • slater determininant
    • normalized
    • permutation operator results in asymmetry
    • when ψ_b = ψ_b meaning same spin: $$\Psi(1,2) = \frac{1}{\sqrt{2}} \begin{vmatrix} \psi_a(1) & \psi_a(2) \\ \psi_a(1) & \psi_a(2) \end{vmatrix} = 0$$

result showing pauli exclusion

16

17 symmetry operations

properties of character tables

• order:
  • using unexpanded symmetry elements using the column: h = Σ_jχ_j²(E) where j represents the irreducible representations
  • using expended symmetry elements (row): h = Σ_Rχ_j²(R) where i is a irreducible representation and R is the expanded row of symmetry elements
• dimension of $j$th irreducible representation: l_j = χ_j(E)

direct sum

• a reducible representation (like MOs) is direct sum of irreducible representations Γ_redu = Σ_ja_jΓ_j = a₁Γ₁ ⊕ a₂Γ₂ ⊕ ...
• where a_j is $$\frac{1}{h} \Sigma_{R} \chi_{redu}(R)\chi_j$$ meaning, sum of product of reducible representation with the representation of the symmetry elemental
• where χ_redu(R) = Σ_j^a_jχ_j(R) is a reducible representation can be further reduced
• to find the direct sum of irreducible representations for a reducible representation, find a_j for all irreducible representations and see which ones are not 0
• χ_j(R) is like a wavefunction that returns the eigenvalue

18

direct product

• a direct product can be reduced to terms of the irreducible representation: Γ_redu = ∏_iΓ_i = Γ_i ⊗ Γ_j ⊗ ... = Σ_ja_jΓ_j
• χ_redu(R) = ∏_iχ_i(R)
• how do we go from direct sum to direct product?

what does direct sum and direct product mean chemically?

• we want to know when two wavefunctions will be orthogonal
  • like frank condon states, we want ⟨Ψ_i|Â|Ψ_j⟩
  • symmetry gives us selection rules

after finding irreducible representation -> SALCs

• we apply the projection operator for SALCs: P̂_j = Σ_j(R)R̂
• for multi-degenerate states, we must orthogonalize to find the right number of wavefunctions

19

20

21

22

23

24

25