CHEM 211: Introduction to Chemical Analysis
2: Equilibrium and Volumetric Analysis
- Recognize compounds that participate in equilibrium reactions or otherwise have an effect on those reactions (e.g., acids, bases, ions that form insoluble or sparingly salts, ligands).
- Define the following terms mathematically and in your own words: Ka, Kb, Kw, Ksp, Kf, Kd.
- $$K_b = \frac{[BH^+][OH^-]}{[B]}$$
- $$K_a = \frac{[A^-][H_3O^+]}{[HA]}$$
- Kw = KaKb
- Ksp = [A+]a[B−]b, solid dissolving into ions
- Kf: formation, ions forming into another ion
- Write mass balance, charge balance and solubility expressions for an equilibrium problem.
- systematic treatment of equilibrium
- as many equations as unknowns
- chemical equilibrium constant expressions
- charge balance charge on cation1[cation1] + charge on cation2[cation2] = charge on anion1[anion1] + charge on anion2[anion2], include every single ion
- formal: moles of original chemical formula in solution, without regard for species that already exist
- how to use:
- mass balance: if you’re looking for a species, check if you set up a mass balance for it, or if you need to sub an unknown
- charge balance: not sure
- chem eq: to sub in an unknown
- Relate physical constants (Ka, Kb, Ksp, Kf) to trends in the shape of titration curves and distribution diagrams.
- Select an appropriate method of endpoint detection and/or indicator (from a limited group of options) for a given analysis and justify your choice.
- equiv points:
- strong acids: 7
- weak acids: pH = pKa at half-equiv point
- endpoints for polyprotic species:
- if $$\frac{K_{a,1}}{K_{a,2}}$$ larger than or equal 104, 1st endpoint will be clear (endpoint can disappear into the other)
- if pKa, 2 less than or equal 8, 2nd endpoint will be clear (if larger than 8, then Ka2 too weak)
- triprotic: third endpoint around 12.7, too small, can’t see
- selecting indicators: pKa of indicator that is close to expected pH at equivalance point
- for weak acid pKa is only half-equiv, so need an indicator that has much higher pKa
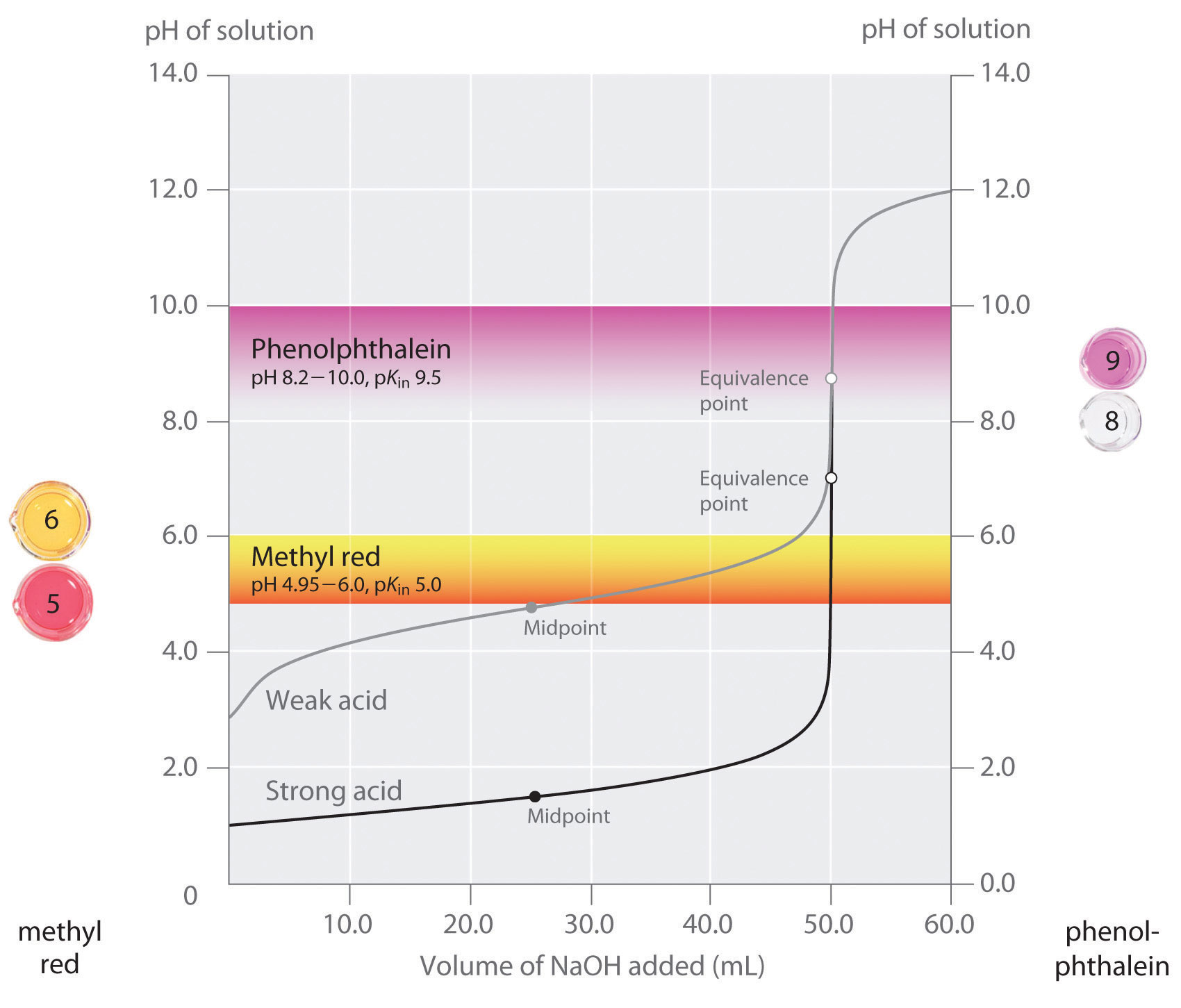
- how to ensure we see the change of color in indicator?
- strong acid: eq point occurs at 7, very steep, the steep portion is almost vertical
- weak acid: Pka of indicator much larger than Pka of weak acid, or indicator changes color too early because not as steep (?), since eq point occurs after pH 7
- weak base: eq point occurs before 7
- Write the equilibrium expression(s) for a complexation titration
- Mm+ + Ln− < − > MLm − n
- $$K_f = \frac{ML^{m-n}}{[M^{m+}][L^{n-}]}$$
- Qualitatively predict the consequences of disturbing a system at equilibrium (e.g., adjustment of pH, changes in concentration, or the addition of new species).
- pH on solubility: using Le Chatelier
- pH increases: adding hydroxide to equation
- pH decreases: adding hydronium to equation
- complexing agent: increases solubility
- Identify relevant equations and make appropriate assumptions to quantitatively analyze an equilibrium system.
misc. info from lectures
- activity
- polyprotic acid
- formulas:
- $$[H^+] = \sqrt{\frac{K_{a2}[HA^-] + K_w}{1 + \frac{[HA^-]}{K_{a1}}}}$$
- $$[H^+] = \sqrt{K_{a2}K_{a1}}$$
- pH = 1/2(pKa1 + pKa2) this is also how you get isoelectric point
- amphiprotic substance
- Henderson-Hasselbalch Equation: $$pH = pK_a + log \frac{[A^-]}{[HA]}$$
- diprotic acid with strong base (how to calculate pH throughout the titration process): (REVIEW)
- buffer region: H-H equation
- compare $Ka$s
- buffers
- effective range: pKa + −1
- gravimetric methods
- obtain analyte by precipitating it
- precipitation titration
- titrant: AgNO3
- argentometric titrations:
- free [Ag+] decreases with small value of Ksp
- small Ksp means bigger number in demoninator (more ppt), pAg is larger
- for titrating: anything that is insoluble when reacted with silver
- endpoint: can be measuring removed or excess
fluorescein:
- titration of halides
- before eq point: colloidal AgX is neg
- after eq point: colloidal AgX is pos
- it depends on the ratio between Ag+ and X− which determines its charge
- titration graph: after eq point, all indicators converge to the same behaviour
- “colloid is a mixture in which one substance consisting of microscopically dispersed insoluble particles is suspended throughout another substance”
- EDTA titration
- how to deal with EDTA titrations at other pH:
- $$\alpha_6 = \frac{[Y^{4-}]}{C_{EDTA}}$$
- from Mn+ + Y4− ⇔ MY(n − 4)+, we get $$K_f = \frac{[MY^{(n-4)+}]}{[M^{n+}] \alpha_6 c_{EDTA}}$$
- complexing agent: EDTA at basic pH
- for titrating: metal
- pH dependence: as pH increases, amount of unbound metal decreases
- auxiliary complexing agent: ammonia to complex cations and maintain solubility at basic pH
- ACA needs larger binding constant than EDTA but smaller formation constant
- why need basic pH? because many metals precipitate as hydroxoides if pH is too high
- concentration of Y−4 is the most at basic pH (it is pH dependent)
- to use a lower pH: need α6, defines mole fraction of Y−4 at given pH
- rewrite MY formation to use α6cEDTA = [Y−4]
- this gives a conditional formation constant: Kf′(pH) = α6Kf
- too much ACA decreases sharpness of endpoint
M2+ + 4NH3 ⇔ Zn(NH3)42+
Zn(NH3)42+ + Y4− ⇔ ZnY2− + 4NH3
- indicators for EDTA:
- Eriochrome Black T: only works on some metals, can use backtitration to use with other metals
- complex titrations
- add masking agents to hide certain metals, needs to have stronger Kf than EDTA
- demasking agent: another metal that binds with masking agent
- auxillary complexing agent: keep metal in solution
- indirect titration
- if titration is slow
- no suitible indicator
- no useful direct titration reaction
- you can add A + B, with B in known excess
- measure leftover B with C
- applications: volhard titration
- titrant: SCN−
- determine: Ag+
- find out how much halide
- indicator: Fe+3
- need to ensure KfAgSCN > KfFeSCN
- back titration for halide determination
- titrate with halide solution with excess Ag
- when all the Cl has been bound, you have Ag in excess
- start titrating the excess Ag with Fe. You add SCN until the solution turns red -> endpoint
- SCN^- turns red at first instance of excess SCN^- by reacting with iron
- displacement titrations
- want to analyse a metal with EDTA, but if the matrix is unknown, other metals may bind to EDTA that is not the metal of interest
- instead, react Ca2+ with MgY+; Ca2+ has higher Kf will displace Mg2+
- titrate the freed Mg2+ in solution ? we titrate the excess Mg with EDTA?
mt1 problems
unit 2
- solubility equilibria: will precipiate form? check if Q > Ksp using the equation [M+][X−]
- solubility equilibria: with x mL 0.y M of MY added to x mL of 0.j M NaI, how much ppt forms and what is the final concentration
- set up reaction equations:
MI ⇔ M+ + I−
MY + NaI ← MI + NaY
- set up Ksp = [M+][I−], find [I−]
- assume [M+] = 0 at eq, so to find [I−], you subtract concentration of M from total concentration of I, then solve for M
- complexation equilibria: what is the concentration of M2+ when x.0 mL of 0.00y M MCl2 is added to z.0 mL of 0.00j M of EDTA at pH 13.0
- set up ice table with starting concentrations, and Kf expression
- mass balance with known concentrations
- assume because of large Kf, [M2+] = 0
- solubility equilibria: solubility of CoCO3 in buffered solution of pH 4.0
- set up equations for Ksp, Ka1, Ka2
- set up mass balance, one for the [Co2+] = ... and [CO32−] = ... and one for the acids
- using known values, substitute and solve for [Co2+]2
- solubility equilibria: solubility of MCl in 0.0x M of NaCN
- given Ksp and Kf, write two equations for each one
- set up mass balance for [M+] and [CN−]
- list assumptions:
- since Kf is large, there is not much free M+
- MCl will dissolve until all CN− used up: [M(CN)2−] > > [CN−]
- [CN−]i = 2[M(CN)2−] = 0.0x M
- [Ag+]i = [Cl−]i = [M(CN)2−]
- XCl is dissolved in a solution of 0.x M ACl, where ACl is soluble and XCl is not very soluble. Given Ksp = [X+][Cl−]
- find equations: ACl ⇔ A+ + Cl−
- set up mass balance: 0.x M = [A+] = [Cl−]total − [Cl−]XCl = [Cl−]total − [X+]
- set up charge balance (include all ions): 1[Na+] + 1[X+] = 1[Cl−]
- check number of unknowns is equal to number of equations
- replace unknowns with known and solve for [X−]
- finding the isoelectric point of an amino acid: $$\frac{1}{2} (pK_{a1} + pK_{a2})$$
- titration of M+ with EDTA at a pH of y, in presence of complexing agent
- solubility of MXs in presence of a complexing agent such as NH4Cl
- indirect titration of A with excess and known B and X: BX binds, then with addition of A, released B is amount of A
- EDTA titration at pH lower than 10: what is the concentration of M2+ when x.0 mL of 0.00y0 MCl2 is added to z.0 mL of 0.0j M EDTA solution buffered at pH k?
- set up Kf expression: $$K_f = \frac{[CaY^{2-}]}{[M^{+2}][Y^{4-}]}$$
- set up mass balance:
$$[EDTA] = \frac{z \times 0.0j \text{ M}}{x + z}$$
$$[MY^{2-}] = \frac{x \times 0.0y \text{ M}}{x + z}$$ assuming all the EDTA forms complex with the metal.
- sub in alpha: [Y4−] = α6[EDTA]free
[EDTA]free = [EDTA] − [MY2−]
- sub in known values into the Kf expression to find the concentration of M2+
$$[M^{2+}] = \frac{K_f \alpha_6 [EDTA]_{free}}{[MY^{2-}]}$$
- argentometric titration before eq point: x mL of 0.0y M XCl was titrated with 0.z M of AgNO3
- find pCl at 10 mL of AgNO3:
- calculate how much Ag+ has been added; this is how much Cl− has formed ppt with silver
- subtract Cl− that has formed complex with Ag+ from initial amount of chlorine
- pCl = log[Cl−]
- argentometric titration at eq: use Ksp
- argentometric titration after eq: calculate excess Ag+, then sub into Ksp expression and solve for [Cl−]

