questions

• what do the different polarizations mean
• what do s and p waves represent

good resources

• https://socratic.org/questions/what-are-the-differences-between-stretching-vibration-and-bending-vibrations

lectures

1: introduction

• basic spectroscopy: light source -> sample -> prism -> detector
  • act of separating light
• history of spectroscopy:
  • 1666 Newton: continuous spectrum of sun
  • 1814 Fraunhofer: found sharp dark lines in sunlight (discrete -> indicts QM)
  • 1900: development of QM
• interstellar molecules (unstable)
• our universe:
  • molecular clouds:
    • very cold: 10 - 100 K
    • not dense: $$\frac{10^{3}}{cm^3}$$
      • this means not many collisions happening, so very unstable molecules can exist <- spectroscopic observation plays important role
  • atmosphere:
    • hot: 300 K
    • dense: $$\frac{10^{20}}{cm^3}$$
• spectroscopy hydrogen atom: chief experimental basis for theories and structure of matter
  • first spectra before QM: Angstrom and Rydberg
  • spectra with QM: Bohr
    • de Broglie: duality of matter $$\lambda = \frac{h}{p}$$ E = hν
    • Schrodinger
  • relativistic quantum theory:
    • Dirac: combine Schrodinger and Einstein
      • $$E = ih \frac{\partial}{\partial \tau}$$
    • Einstein: relativity (things moving at speed of light)
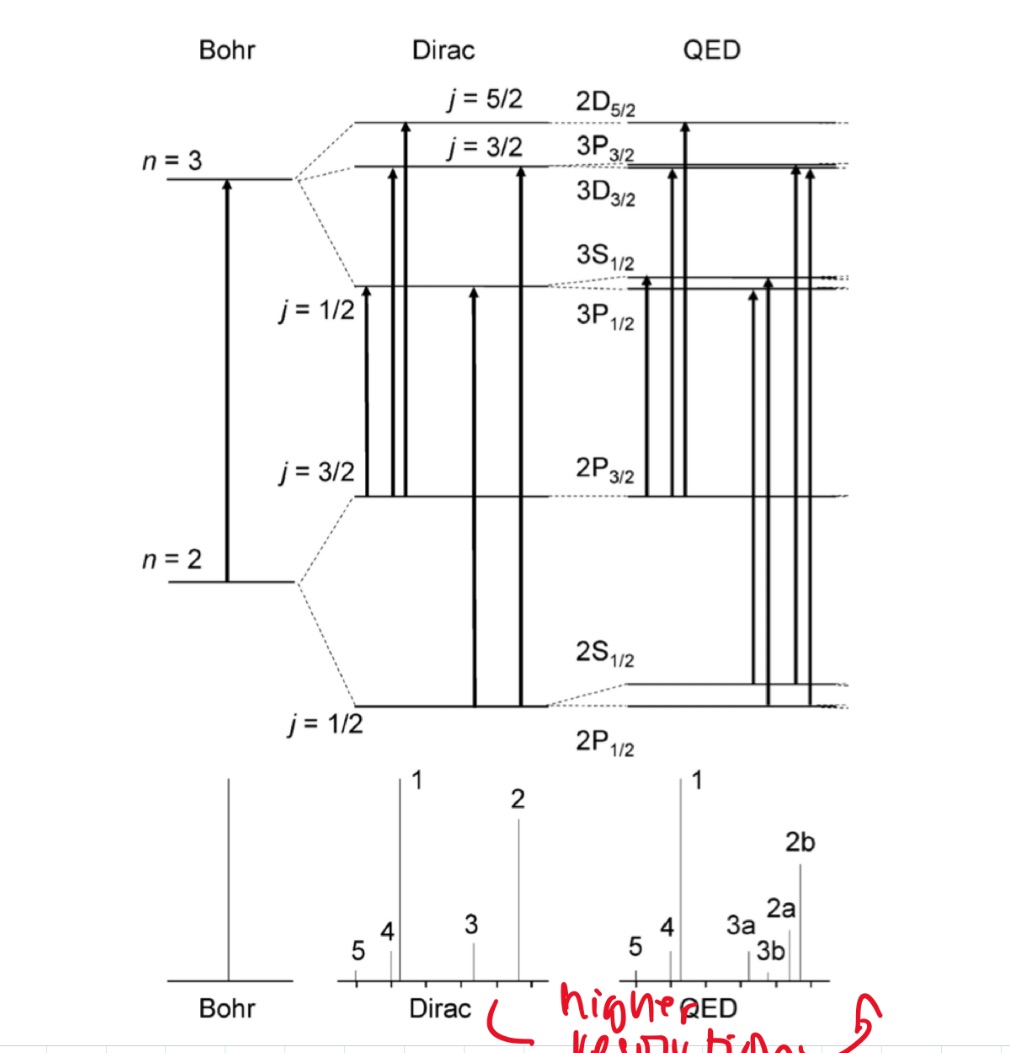
• splitting of hydrogen: bohr -> dirac -> qed

2: WebMO practice

• dihedral angle: rotate relative to a plane
• linear molecule: 2 rotational constants
• non-linear molecule: 3 rotational constants
• first optimize then calculate vibrational frequency

3: intro to QM

4: intro to EMR

electromagnetic radiation

• electric () and magentic () fields pervade all space; they are vectors with three components (x, y, z)
• in vacuum, speed of light is 2.998 × 10⁸ m/s
• general form: E(r, t) = E₀cps(wt − k dotr)
  • where E₀ is the amplitude vector, k is propagation vector, with r being vector containing x, y, z
• planck relation: $$E = hv = \hbar w = \frac{hc}{\lambda}$$
• 1 eV  = 1.602 × 10⁻¹⁹ J  = 8065.54 cm ⁻¹

1. fields (EMR fields)

   • 6 fields that are related by these two equations: $$ \vv{D} = \epsilon \vv{E} = \epsilon_0 \vv{E} + \vv{P}$$ $$ \vv{B} = \epsilon \vv{E} = \mu_0 \vv{H} + \vv{M}$$
   • $$\vv{E}$$ and $$\vv{H}$$ (electric and magnetic field) are perpendicular to each other and the propagation vector $$\vv{k}$$
     • $$H_0 = \sqrt{\frac{\epsilon}{\mu}}E_0$$

2. polarization of light

   • light is transverse wave: osciallations of $$\vv{E}$$ and $$\vv{H}$$ are perpendicular to propagation direction
     • $$ k = |\vv{k}| = \frac{2 \pi}{\lambda} = \frac{w}{c}$$
     • still have DOF in plane perpendicular to $$\vv{k}$$, which relates to the polarization of light
       1. unpolarized light: no perferred direction for $$\vv{E}$$, can be any direction perpendicular, is a statistically mixed state
       2. polarized light: the polarization of $$\vv{E}$$ can rotate during oscillation, the angle
          • for light in the z direction: (E_x0cos(kz − wt), E_y0cos(kz − wt + θ), 0)
            1. plane/linearly polarised: θ = 0
            2. elliptically polarized light: $$\theta = +/- \frac{\pi}{2}$$, and E_x0 ≠ E_y0 left/right hand
            3. circularly polarized light: E_x0 = E_y0, L/R

3. angular momentum and light

   L/R circularly polarized photons have angular momentum +/ − ℏ

   • no S_z = 0 photons as light must remain transverse (what does this mean)
     • photon is a massless particle, don’t actually haves spin
       • have helicity: value of projection of spin operator onto the momentum operator
   • unpolarized light: random statistical mixture of L/R
   • polarised light: coherent superposition of L/R circularly polarized light

4. propagation of light

   • speed of light in vacuo: $$c_0 = \frac{1}{\sqrt{\epsilon_0 \mu_0}}$$
   • speed of light in medium: $$c_0 = \frac{1}{\sqrt{\epsilon \mu}}$$ where ϵ and μ are characteristic to the medium
   • refractive index: $$n = \frac{c_0}{v} = \sqrt{\frac{\epsilon \mu}{\epsilon_0 \mu_0}} \geq 1$$, where μ is magnetic permittivity
   • for nonmagnetic media: $$n = \sqrt{\frac{\epsilon}{\epsilon_0}} = \sqrt{\epsilon_r}$$, where ϵ_r is the relative electric permittivity
     • dielectric constant: measured by response to static/low frequency electric field

5. reflection and refraction

   • frequency (energy) is unchanged from vacuum value when passing through a medium, v = v₀, so since c = c₀/n: the wavelength is reduced: λ = λ₀/n
     • $$E = hv = \frac{c_0 / n}{ \lambda_0 / n}$$
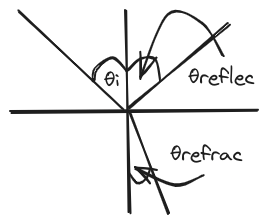
   • reflection (specular, meaning mirror like): θ_inc = θ_refl
   • refraction (snells law): n₁sinθ_inc = n₂sinθ_refr
   • polarization:
     • determines the reflectivity
     • R is reflectance, T = 1 − R is the transmittance
     • for s and p waves: with T = 1 − R
     • Fresnel equation
       • $$R_s = |\frac{n_1 cos \theta_i - n_2 cos \theta_t}{n_1 cos \theta_i + n_2 cos \theta_t}|^2$$
       • $$R_p = |\frac{n_1 cos \theta_t - n_2 cos \theta_i}{n_1 cos \theta_t + n_2 cos \theta_i}|^2$$
       • another form:
         • $$R_s = |\frac{sin(\theta_2 - \theta_1)}{sin(\theta_2 + \theta_1)}|^2$$
         • $$R_p = |\frac{tan(\theta_2 - \theta_1)}{tan(\theta_2 + \theta_1)}|^2$$
       • normal incidence: θ_i = θ_t = 0, then $$R = R_s = R_t = (\frac{n_1 - n_2}{n_1 + n_2})^2$$
       • total internal reflection: when n₁ > n₂, there is a critical angle, which R_s, R_t = 1
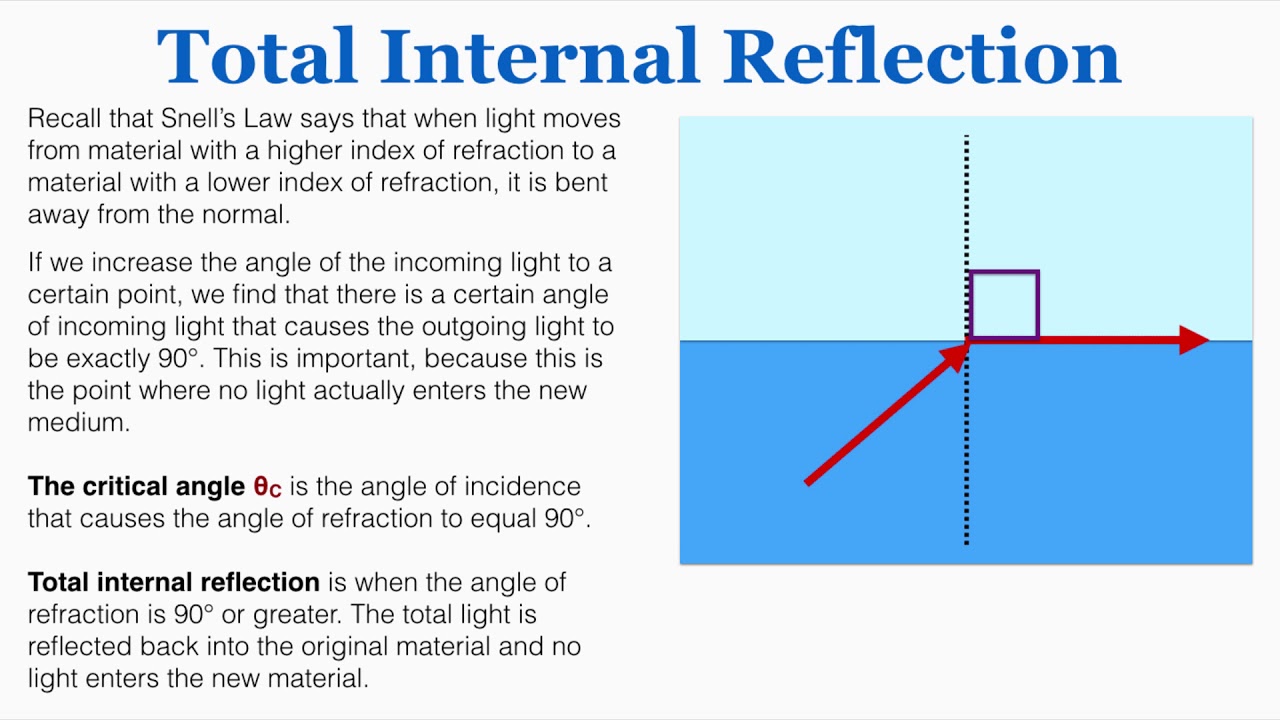
   • brewster’s angle: when θ_t + θ_i = 90^deg R_p → 0 and T_p → 1, p polarized light will not be reflected, or if the incident light is unpolarized, only s polarized light will reflect, this is how you can produce polarized light
     • θ_B = arctan(n₂/n₁)
     • no reflection for p wave
   • dispersion
     • sellmeier equation (empirical relation between n and λ)
   • absoption and refractive index
     • normal regions of dispersion separated by regions of anomalous dispersion between different regions of NMR spectrum
     • kramers-kronig index
   • birefringence
     • refractive index: depends on angle between polariztion of light and crystal axis

5: light-matter interaction

radiation density and intensity of light

• let ρ be volume density of energy in EM radiation J/m³
• to find contributions at various frequencies ρ(v) is energy density per unit frequency, and $$ ρ = ∫₀^inf  p(v) dv$
• intensity of light: I = ∫₀^infI(v)dv
• photon flux: number of photons flowing through a unit area per unit time $$F = \frac{I}{(hv)}$$
  • relations: I(v) = p(v)c = p(v)(c₀/n)
  • $$I(v) = \frac{1}{2} \epsilon_0 E^2_0 c$$, where E₀ is the amplitude for electric field osciallations at frequency v

absorption and emission

• consider a two level system: can have three processes:
  1. absorption
  2. spontaneous emission
  3. stimulated emission

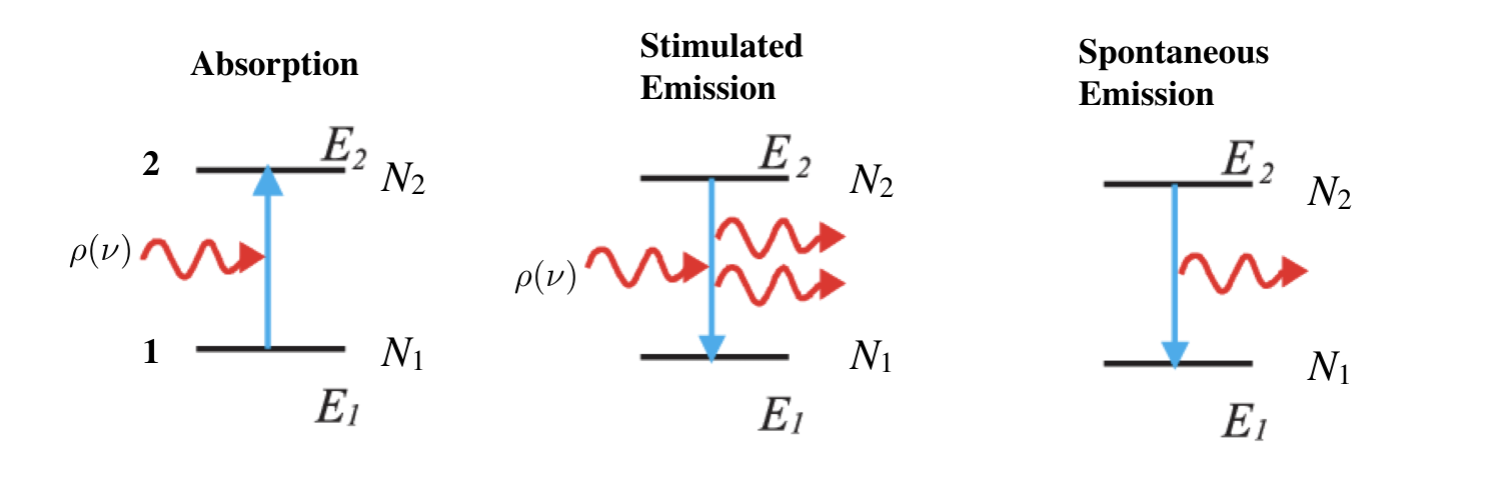
• A and B are transition probabilities, N₁, N₂ are populations
• Einstein’s treatment: @ thermal equilibrium, population ratio given by Boltzmann factor, with degeneracies g: $$\frac{N_2}{N_1} = \frac{g_2}{g_1} e^{-hv / kT}$$, where hv = E₂ − E₁
• spontaneous decay (no radiation) kinetic rate law: $$\frac{-d N_{2}}{dt} = A_{21}N_{2}$$, N₂(t) = N₂(0)e^−A₂₁t, so radiative lifetime of excited state is $$\frac{1}{A_{21}}$$
• with radiation:
  • upward transition: W₁₂ = N₁B₁₂ρ(v)
  • downward transition: W₂₁ = N₂B₂₁ρ(v) + N₂A₂₁
  • at eq: these two rates must be equal, so we can solve for ρ(v) and insert the thermal eq Boltzmann factor and equate to thermal blackbody spectrum:
    • $$\frac{A_{21}}{(g_1/g_2) e^{\frac{hv}{kT}} B_{12} - B_{21}}$$
    • we get g₁B₁₂ = g₂B₂₁: equal probability of 1 to 2 or 2 to 1
    • and $$\frac{A_{21}}{B_{21}} = \frac{8 \pi h v^3}{c^3} \propto v^3$$
      • higher frequency: spontaneous emission
      • lower frequency: stimulated emission

transition dipole momentum

• transition rate determined by “transition dipole moment”
• transition dipole moment between two states n and m is a vector: $$\mu_{mn} = \int \psi_m^* \hat{\mu} \psi_n dV = \langle m | \hat{mu} | n \rangle $$
  • $$\hat{mu}$$ is the electric dipole moment operator: $$\hat{mu} = \sigma_i q_i r_i$$
• transition rates determined by Einstein coefficients times a lineshape factor resonantly peaked at transition frequency (E₂ − E₁), enforces energy conservation

beer’s law

• not covered much, study more later

line profiles for spectral lines

• conservation of energy: v = v₁₂: $$v_{12}$ splittings between eigenvalues - $$δ(v - v₁₂)$$
• reality: emission/absoption never perfectly monochromatic (single wavelength/color): each line has characteristic shape/profile, with certain width δv, quantified as FWHM
• lines spaced apart less than δv cannot be seperated/resolved
• common line shape:
  • lorentzian: broadening by the natural lifetime of the excited state
  • guassian: inhomogeneous broadened lines (Doppler broadening)
  • voigt: mixes guassian and lorentzian
    • convolution of two and appropriate when homogeneous and inhomogeneous mechanisms are important
• natural linewidth

6: prep for final presentation

8: molecular symmetry and group theory 1

• operators:
  • Ê is identity operator

9: molecular symmetry and group theory 2

• group theory and quantum mechanics
  • point symmetry operator R
    • representation of R based on point in 3D space: real orthogonal 3 × 3 rep M = Γ(R)
    • symmetry operations as operators on space of wavefunctions
      • generalization of symmetry on arbitrary point: $$r = M r = \begin{bmatrix} x^, \\ y^, \\ z^, \end{bmatrix}$$
      • we can define the operator P̂_R by
        • P̂_R|ψ⟩ = P̂_R|ψ(x, y, z)⟩ = |ψ(M⁻¹r)⟩=|ψ(x^,, y^,, z^,,)⟩
      • interested in finite dimensional subspace of Hilbert space (5D space spanned by 3d orbitals): basis set is set of solutions of Schrodinger equation, eigenfunctions of Ĥ
• symmetrization
  • projection operator $$\hat{P^{\mu}}$$: annihilates all functions that does not belong to μ-th irreducible representation

10: molecular rotation and spin statistics 1

11: molecular rotation and spin statistics 2

born-oppenheimer approximation

• fixed nucleus
• total hamiltonian consists of kinetic energy of nucleus, electrons, and coloumb potential energy between nuclei, nuclei-electrons, and electrons

(and BO adiabatic approximation)

• wavefunction is product of electron and nuclei Ψ_n, i = χ_i⁽ⁿ⁾(R)ψ_n^el(r; R)
• for a fixed R we get the electronic schrodinger equation: Ĥ = Ĥ_nuc + Ĥ_elec, where Ĥ_elec = ψ_n^el(r; R) = E_n^el(R)ψ_n^el(r; R)
• nuclear schrodinger equation: [Ĥ_nuc + E_n^el(R)]χ_iⁿ(R) = E_{n, iχi⁽ⁿ⁾}(R)
  • then by changing the value of R, we get the potential energy surface E_n^el

separation of vibration and rotation

• separation of translational motion
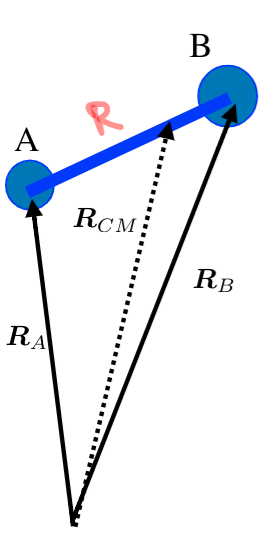
  • we can seperate translational motion and internal motion (rotation and vibration) by using R_CM, center of mass
• $$\hat{T}_{nuc} = - \frac{\hbar^2}{2M} \nabla^2_{CM} - \frac{\hbar^2}{2 \mu} \nabla^2_{int}$$

can further seperate vibrational and rotational motion

• using polar coordinates
  • $$\hat{H}_{nuc} + E^{el}_n (R) = \hat{T}_{vib} + E^{el}_n (R) + \frac{1}{2 \mu R^2} \hat{L}^2 (\theta \psi)$$ (last term is Ĥ_rot)
• we get vibration-rotation wavefunction: χ_{n, v, J, M}(R) = S_v⁽ⁿ⁾(R)Y_JM(θψ) where vibration only depends on bond length and rotation depends on two angles

rotation of diatomic molecules

• rigid rotater: if you set R = R_e where R_e is equilibrium bond length, T̂_vib = 0
• spherical harmonics (eigensolution)
• for L̂²|Y_Jm, ℏ²J(J + 1) is the eigenvalue
• for L̂_z, ℏm is the eigenvalue
• moment of interia is simple I_e = μR_e²
• rotational constant:
  • $$B_e = \frac{\hbar^2}{2 I_e} \text{ (J)}$$
  • $$ = \frac{\hbar^2}{8 \pi^2 I_e} \text{ (Hz)}$$
  • $$ = \frac{\hbar^2}{8 \pi^2 I_e c} \text{ (cm}^{-1})$$

polyatomic molecules: linear

• start with moment of inertia tensor: $$\begin{bmatrix} I_{xx} & I_{xy} & I_{xz} \\ I_{yx} & I_{yy} & I_{yz} \\ I_{zx} & I_{zy} & I_{zz} \\ \end{bmatrix}$$
• diagonalize to get moment of intertia: $$\begin{bmatrix} I_{aa} & & \\ & I_{bb} & \\ & & I_{cc} \\ \end{bmatrix}$$
• x y z axis don’t always correspond to a b c axis
• to calculate:
  • I_xx = Σm_α(y_α² + z_α²)
  • I_xy = −Σm_αx_αy_α
• example:
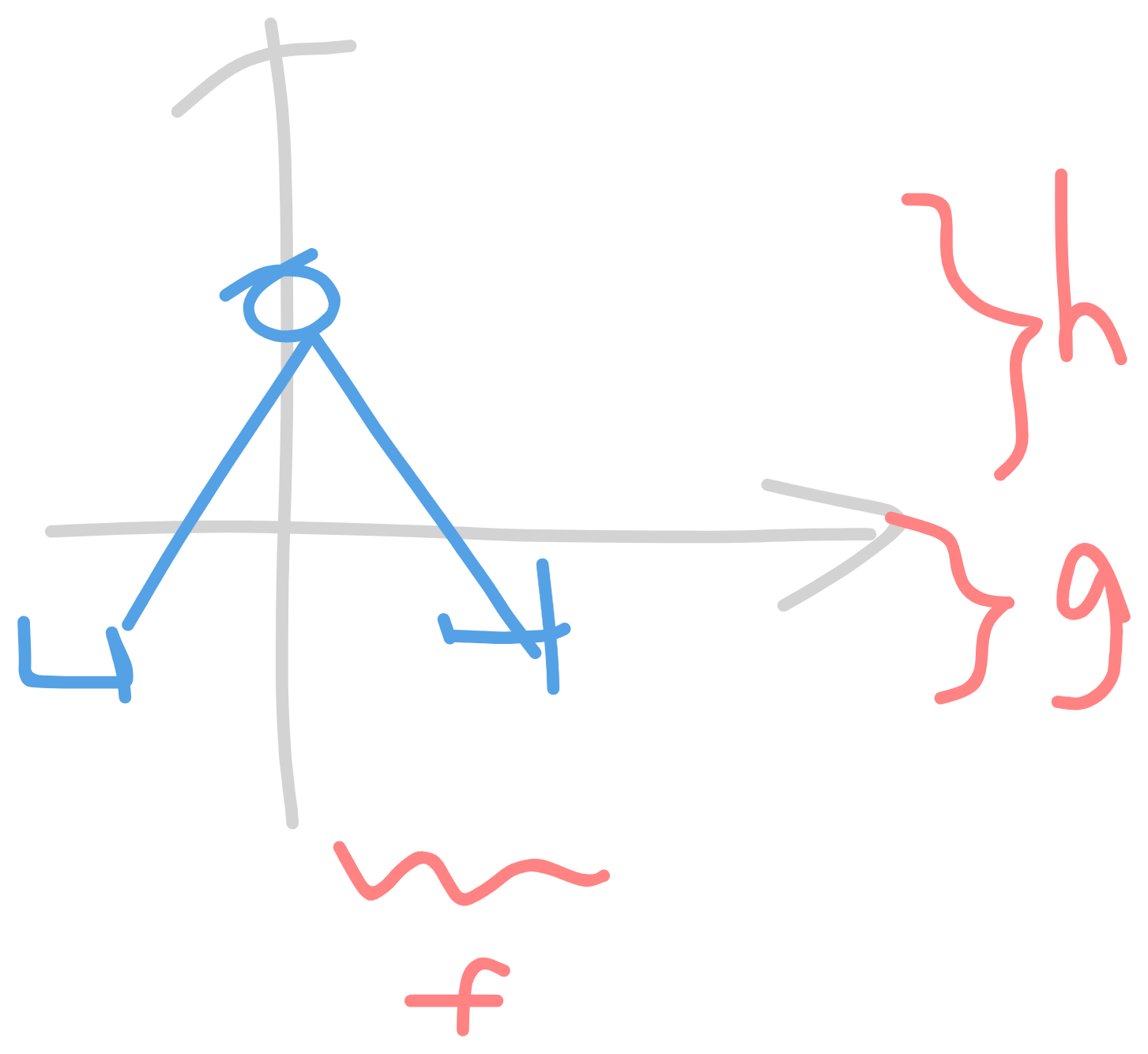
  • I_xx = Σm_α(y_α² + z_α²) = M_H(f² + g²) + M_H(f² + g²) + M_Oh²
  • I_xy = −Σm_αx_αy_α = −(M_Hfg + M_Hf(−g)) why no M_O
  • $$\begin{bmatrix} M_H h^2 + 2M_H (f^2 + g^2) & 0 & 0 \\ 0 & M_O h^2 + 2 M_H g^2 & 0 \\ 0 & 0 & 2M_H f^2 \\ \end{bmatrix}$$
  • 3 moment of inertia values, 3 rotational constants
    • units of inertia: $\text{amu} \AA^2$
      • I_A ≤ I_B ≤ I_C, A ≥ B ≥ C
    • rotational constant $=505379.07/I amu Ų$$
• important quantum notes:
  • I_a = 0, I_b = I_c
  • degeneracies: g = 2J + 1
  • E_J = BJ(J + 1)

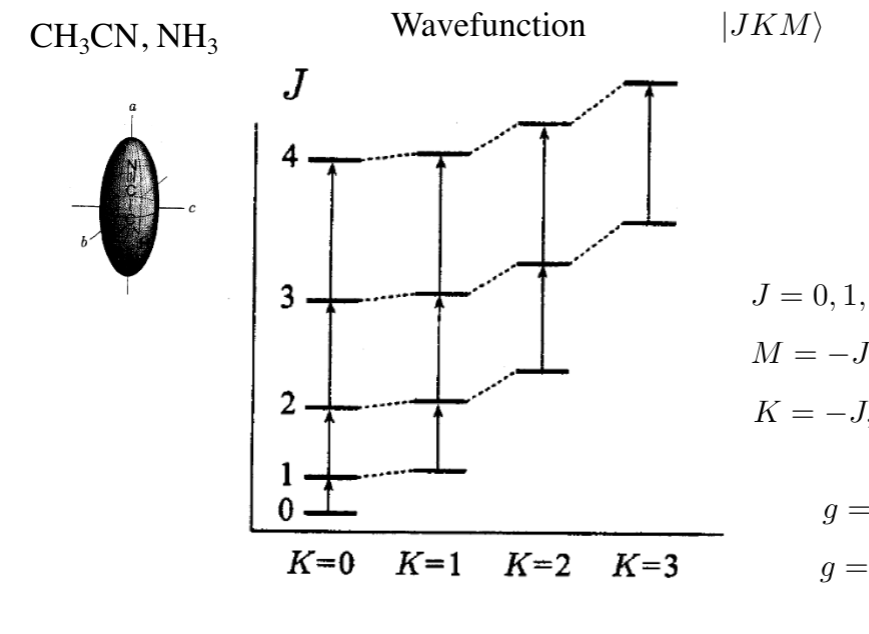
polyatomic molecules: symmetric top

• prolate: I_a < I_b = I_c, A > B = C
• another quantum number: J = 0, 1 2, and K, M = -J, -J+1, …, J-1, J
  • if K = 0: g = 2J+1
  • if K != 0: g = 2(2J+1)
• E_JK = BJ(J + 1) + (A − B)K²

• oblate: I_a = I_b < I_c, A = B < C
• E_JK = BJ(J + 1) + (C − B)K²

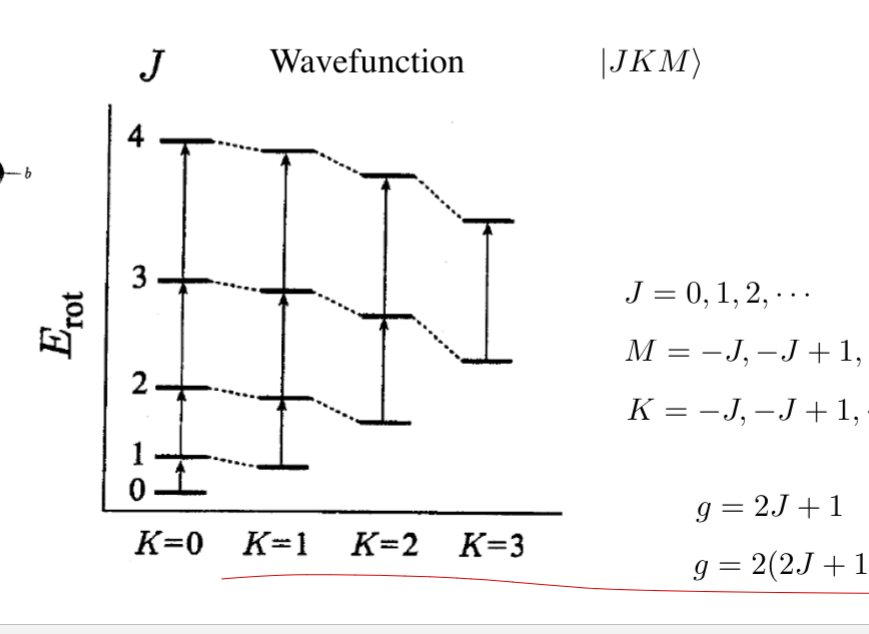
polyatomic molecules: spherical top

• I_a = I_b = I_c

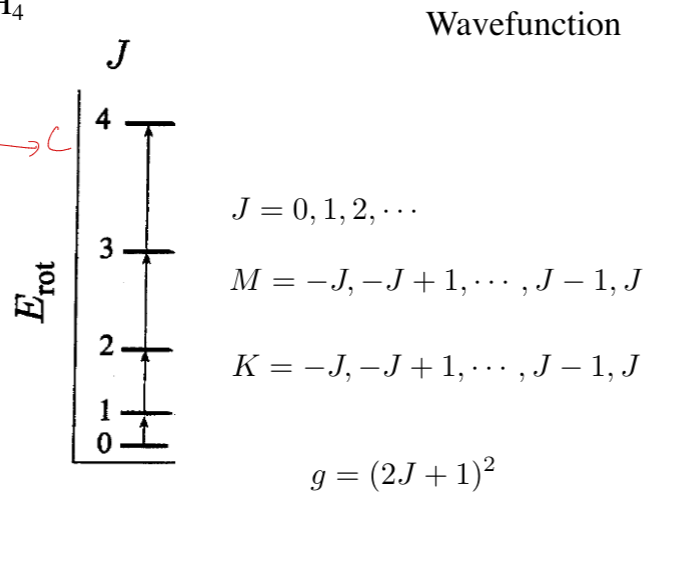
• E_J = BJ(J + 1)
• there is still K, g = (2J + 1)²

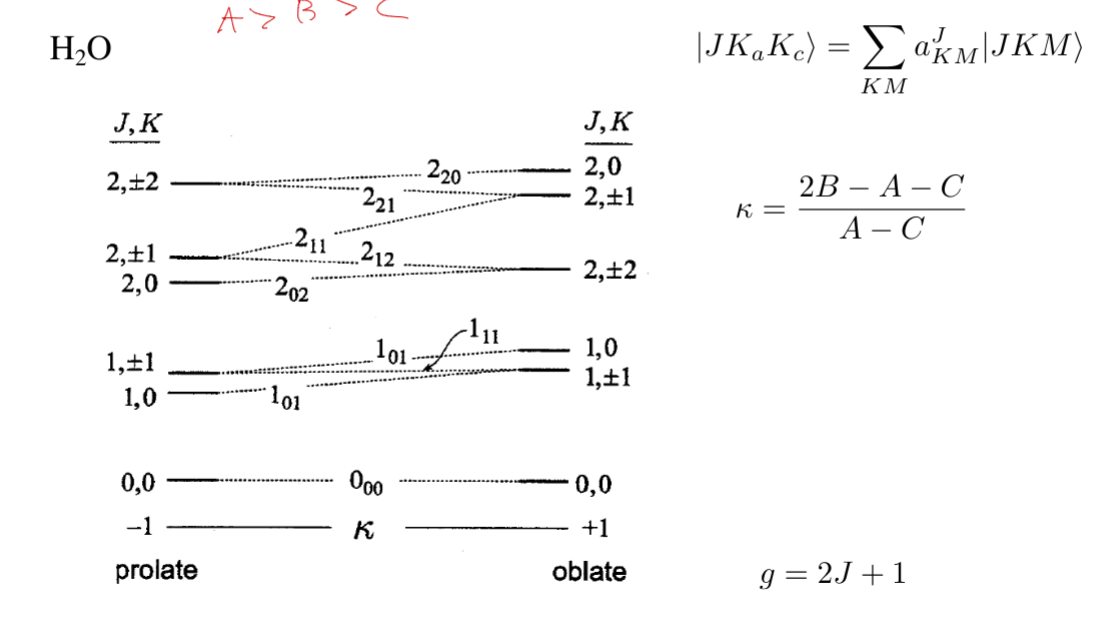
polyatomic molecules: asymmetric top

• I_a ≠ I_b ≠ I_c

optical selection rule: diatomic and linear

• μ₀ ≠ 0 ΔJ = +/ − 1, ΔM = 0, +/ − 1
  • can only transition between J and J+1, separations are 2B.
  • transition frequency: 2B(J + 1)

symmetric and asymmetric top molecules

• symmetric top: μ₀ ≠ 0 ΔJ = +/ − 1, ΔM = 0, +/ − 1, ΔK = 0
• asymmetric top: ΔJ = 0, +/ − 1, ΔM = 0, +/ − 1
  • then more details based on if it is a-type, b-type, c-type transition

general notes

• no dipole moment, no transition (mu cant be 0, mu is dipole moment)

12: molecular vibration

• we can get the vibrational schrodinger equation by representing in polar coordinates: $$[-\frac{\hbar^2}{2 \mu} \frac{\partial^2}{\partial q^2}]\phi_v^{(n)} = E^{(n)}_{vib, v} \phi^{(n)}_v$$
• D_e is equilibrium dissociation energy (bond dissociation energy)
  • associated with equilibrium bond distance
  • D_e − ZPE = D₀
• D₀ is dissociation energy (chemical-dissociation energy), true ground state energy

harmonic oscillator model

• taylor series around R_e
  • 0 potential at R_e
  • first derivative is 0 (this is set, to find eq point)
  • harmonic potential: $$V(q) = \frac{1}{2} (\frac{d^2 V}{dq^2})_0 q^2 = \frac{1}{2} kq^2$$
    • classical: $$T + V = E = \frac{1}{2} k x_0^2$$
    • quantum: $$E_v = (v + \frac{1}{2}) hv_0$$, and the Hamiltonian: Ĥ = T̂ + V̂

selection rule

• within the same electronic state (which means? same quantum numbers): Δv + / − 1, and $$\frac{df \mu_0}{dq} \neq 0$$, there must be dipole moment/must be polar
  • fundamental: 1 ← 0
  • hot bands: 2 ← 1 observed when its really hot
  • overtone: 2 ← 0 (2 times the fundamental frequency)

rotation-vibration transition (diatomic molecules)

• energy: $$E_{vJ} = (v + \frac{1}{2}) h_{v_e} + B_e J (J+1)$$ first term (vibration) + second term (rotation)
• rotational: ΔJ = +/ − 1 ΔM = 0, +/ − 1, ΔJ = 0, +/ − 1 if L, S ≠ 0
• vibrational: δv = +/ − 1 and dipole moment cant be 0
  • types of branches:
    • P branch: v_{J − 1 ← J},
    • Q branch: v_J ← J, ΔJ = 0
    • R branch: v_{J + 1 ← J}, ΔJ = +1

vibration of polyatomic molecules

• for each atom, you get one coordinate, then you get $$\hat{T}_vib = \frac{1}{2} \Sigma q^2_i$$
  • do taylor expansion, then you get hessian matrix, b_ik
    • normal modes: coordinate system that make b_ik diagonal

vibrational levels

• fundamental: one quanta change
• overtone: two quanta change
• combination: different modes all transition
• energy of all vibrational modes: $$\Sigma_i (n_i + \frac{d_i}{2}) v_i$$
  • total zero point: $$\frac{1}{2} (v_1 + ... v_n)$$

other info

• C-H stretch: 2700-3100 1/cm
• O-H stretch: 3580 - 3650 1/cm

normal modes

• to determine how many of each normal mode you have
  • translational: always 3 (x,y,z)
  • rotational: (R_x, R_y, R_z):
  • left over is vibrational

symmetry of vibrational wavefunction

• ground state is always (0,0,0,…)
• two quanta of B₂ gives A₁

13: vibrational infrared and raman spectroscopy

scattering:

• incident beam gets scattered by a medium, producing wavelengths of ??? frequency in all directions ??? is the frequency the same or different
  • stokes: lower frequency
  • anti-stokes: higher frequency

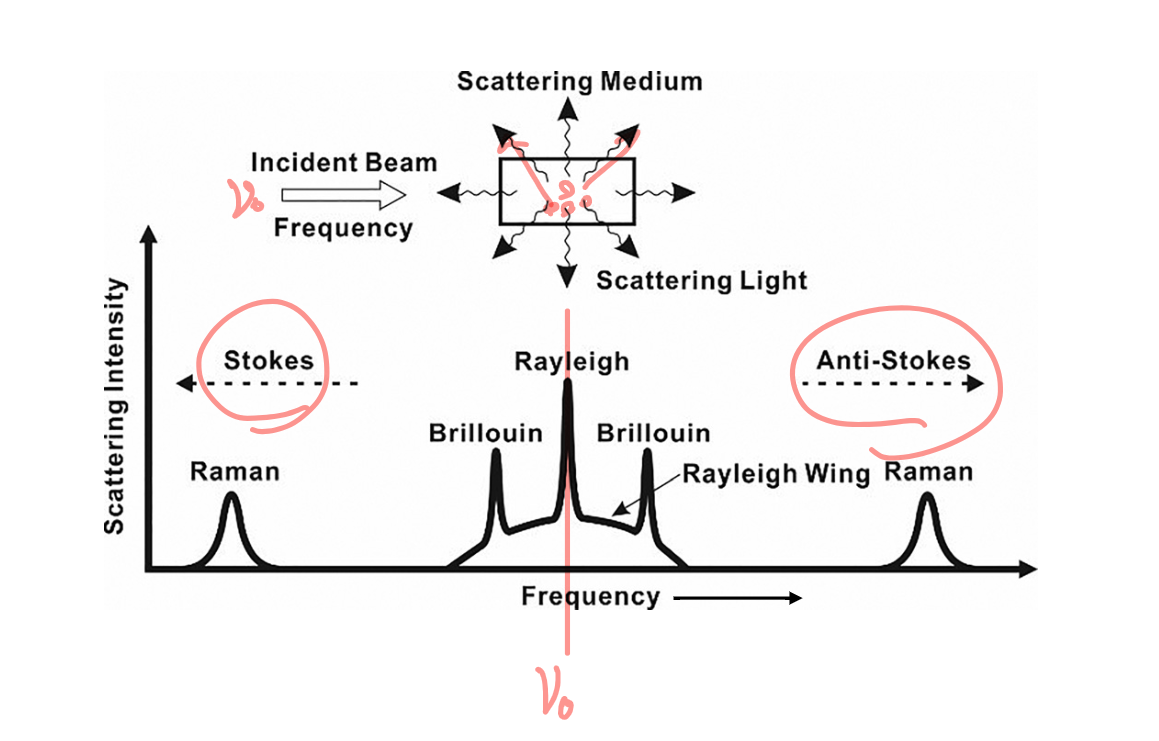
• rayleigh scattering: object much smaller than wavelength
• mie scattering: object larger than wavelength
• brillouin scattering: condensed phase, less dense phase is same size as wavelength

raman

• two photon scattering
• scattered photon loses energy, and there is intermediate state
  • final energy is higher than initial: stokes
  • final energy is lower than initial: anti-stokes
• $$\frac{\partial \alpha}{\partial R} \neq 0$$, must be nonpolar
  • ⟨i|α|f⟩
• excitation wavelength doesnt matter, always produces same output

resonant raman scattering:

• wavelength is same as excitation wavelength

14: electronic spectroscopy

atoms

• sharp spectra
• with many electron atoms, coupling occurs
  • J-J coupling: heavy atoms
  • L-S coupling: light atoms
• total angular momentum: Ĵ = L̂ + Ŝ
• why loss of degeneracy caused by coulomb interaction
• Hund’s rule
  • state with largest S most stable
  • for same S, state with largest L is most stable
• ^2S + 1L_J
  • $\hat{H}_{so} = \zeta \hat{L} \dot \hat{S}$: represented by J
  • Ĥ₀ + Ĥ_ee + Ĥ_so

SO splittings:

• energy difference: $E_{J+1} - E_J = \frac{1}{2} \zeta [(J+1)(J+2) - J(J+1)] = \zeta (J+1)$

selection rule

• dipole transition: $\hat{mu} = - e r$, Δm_s = 0, Δl = + − 1 dipole moment, Δm_l = 0, + − 1, Δn any positive integer

15: electronic spectroscopy

16: magnetic resonance

17: spectroscopy

18 - 25:

Two-photon doppler free spectroscopy

REMPI (Resonant Enhanced MultiPhoton Ionization)

• two photons required
• excite molecules into excited state followed by ionization
  • stepwise ionization (minimum of 2 photons)
  • ionization rate higher when photons in resonance with intermediate state
  • TOF for mass spec
• need tunable light source (dye laser), ion yield vs. wavelength is plotted
• shows same feature as absoption spectrum
  • different set of selection rules -> transitions forbidden with one photon are not forbidden with two photons
• multiple photons can be absorbed: ionization at less energetic wavelengths
  • can excite different energy levels with same ionization
• all photons emitted are same energy: is this always the case?
  • total energy doesn’t need to equal the ionization energy

Saturation absorption spectroscopy

Fluorescence correlation spectroscopy

Cavity ring down spectroscopy

Frequency comb spectroscopy

Coherant Anti-Stokes Raman spectroscopy

Fluorescence resonance energy transfer spectroscopy

Photoelectron velocity map imaging spectroscopy

Two-dimensional infrared spectroscopy

Multi-dimensional NMR spectroscopy

Scanning near field optical spectroscopy

Optical coherence tomography

• high resolution, non-invasive of biological tissue
• interferometry:
  • split beam of light
• low coherence: control interference
  • long coherence: lots of interference
  • short: interference only at specific z
• image generation: A, B, C scan
• resolution: axial and transverse (independent)
• comparison: confocal (limited depth), ultrasound (low resolution/lots of depth), optical coherence (in the middle)
  • question: combine confocal + ultrasound?

Positron emission tomography

THz spectroscopy and Imaging

Atto-second time resolved spectroscopy

Operando spectroscopy

Circular dichroism spectroscopy, optical rotatory dispersion

Raman optical activity